Post by IgnacioMira, esto es un problema interesante.
Puede, mientras quede claro que es otro problema completamente diferente.
Post by Ignacio¿Quieres decir que una masa de (a ver, wikipedia--> 5.9742×10E24 kg)
de H2O puro orbitando el Sol a 1 u.a. no sería estable? ¿Por qué?
No, no quise decir eso.
Hablabamos de un planeta de agua en forma liquida, recuerda que se
trataba de cuanto tardaba una bola de acero, y entiendo que con el mismo
tamaño que la Tierra.
Un planeta completamente hecho de h20 con la misma masa que la Tierra,
es otra historia bastante diferente a discutir.
Post by IgnacioLo único que se me ocurre es que el viento solar y el calor le hagan
perder masa desarrollando una megacola como un cometa[1], pero un
cometa de ese tamaño duraría muuuucho.
Un planeta como la Tierra entiendo que tiene la orbita de la Tierra,
pero si ademas de cambiarle la composicion, el tamaño, lo quieres ademas
alejar del sol, cambiando su temperatura, ya le queda poco de "como la
Tierra".
Post by IgnacioDesde luego, en el centro de la masa habría una presión y una
temperatura muy altas, y ni quiero pensar en un modelo de convecciones,
turbulencias, las distintas fases del hielo posibles según la zona,
capas de hidrógeno escindido en el núcleo, complicaciones varias.
La densidad media de la Tierra, es de 5.5 g/cm^3 aunque varia entre 1.2
en superficie y 14 en el nucleo. Esta compuesta de materiales casi todos
mas pesados que el agua en condiciones normales. Estatanto en forma
liquida como solida tiene una densidad en torno a 1 g/cm^3 (a presion
ambiente).
Loading Image...
Pero todo varia con la presion. En realidad la variacion de densidad de
la Tierra se debe muchisimo a variaciones de composicion. La Tierra de
hielo podria parecer un modelo bastante mas simple, pero no lo es tanto.
La presion en el nucleo terrestre llega hasta los 300 GPa, a estas
presiones _todo_ es compresible, ya no solo los liquidos, sino los
solidos tambien y por supuesto el agua y el hielo.
Solo he encontrado datos experimentales de la densidad del hielo hasta
160 Gpa (no he buscado mucho tampoco). Su parametro de celda de red
(cristalina) pasa de 3.4 A a 2.5A, asi que es de esperar que se
triplique su densidad a 160 GPa. Su densidad se puede multiplicar mas o
menos por cinco a 300 GPa.
Loading Image...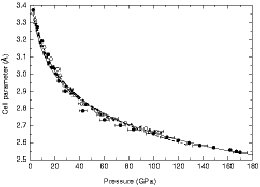
Si fijas la masa total de la tierra deberias determinar su radio. Para
ello hay que saber la funcion de compresibilidad del hielo. Hay que
saber cuanta presion hay a cada profundidad, la cual depende de cuanto
sea de compresible, porque la densidad y la gravedad del planeta en el
interior va variando tambien con el radio. Pero es un problema mixto de
cristalografia y gravitacion (y si nos ponemos cuantico, puesto que
necesitamos el parametro de red del enlace)
No es dificil de resolver con un par de integrales en esfericas (si
alguien quiere intentarlo como ejercicio) aproximando el parametro de
red por una funcion exponencial (no es exacto, porque a mayor presion se
desvia).
Pero lo que quiero señalar es que necesitamos considerar las fases
cristalinas y todo para saber simplemente el tamaño que puede tener ese
planeta. Y no podemos descartar dinamicas complicadas de diferentes fases.
Y me he dejado la temperatura aparte que no es cosa despreciable.
Ese h20, cuanto deuterio y tritio contiene?
El calor en el nucleo terrestre no debe mucho a las desintegraciones
radiactivas, comparado con lo que debe al sol, pero si no tienes otra
fuente...
Hay que estudiar la conductividad termica del hielo (de nuevo un
problema de estado solido) para saber a que ritmo se enfriaria este planeta.
Luego encima las fuerzas de marea probablemente partirian en trocitos
una estructura completamente cristalina. Un planeta rigido tiene muy
pocas posibilidades de aguantar como un monocristal todo el tiempo.
Estaria fracturandose constantemente con una dinamica muy complicada.
Probablemente esto causaria cambios de fase a liquido en algunas zonas.
Post by IgnacioY sin dua, en el Cinturón de Kuiper duraría todo el tiempo que se
quisiera. Igual algún día nos encontramos un objeto así: ya están
insinuando que esperan encontrar un "Mercurio" o un "Marte", al menos
de diámetro si no de masa.
Si pero no de H20 puros, cuanto mas grande sea la roca, mas improbable es.
Una piedra de hielo relativamente pequeña es una cosa, pero un planeta
del tamaño o la masa de la Tierra es una cosa muy grande donde la alta
gravedad complica mucho las cosas. Es muy dificil ademas que
espontaneamente se forme un planeta "puro" de un solo material ya que
todos tienden a condensar en su nucleo los materiales mas pesados por
sedimentacion. Tendria que formase por las buenas en una region del
espacio donde solo hubiese hidrogeno y oxigeno, y nada mas.
Y todo eso sin siquiera considerar ni su rotacion, ni la radiacion solar.
Estamos hablando de toda una geologia planetaria bastante exotica.